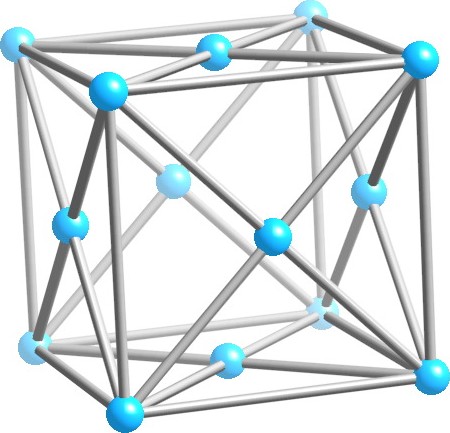
アルミニウム結晶の電子状態計算
アルミニウム結晶は面心立方格子であり、その格子常数(上記のような立方体の単位格子をとったときの一辺)は0.40496nm(4.0496Å)である。原子間距離や面間隔を確認せよ。
実習1
- アルミニウム結晶の電子状態を計算するためのpythonスクリプトを作成し計算を実行せよ
FCCの単純単位格子
単位格子を立方体の形にとると、1つの単位格子に4つの原子が含まれている。1つの単位格子に1つの原子が含まれるように単位格子をとるには、
$$ \begin{array}{l} \vec{a}_1=(0,\,\displaystyle\frac{a_0}{2},\,\frac{a_0}{2})\\ \vec{a}_2=(\displaystyle\frac{a_0}{2},\,0,\,\frac{a_0}{2})\\ \vec{a}_3=(\displaystyle\frac{a_0}{2},\,\frac{a_0}{2},\,0)) \end{array} $$
のように単位格子ベクトルをとればよい。したがって、計算で用いるAtomsオブジェクトは
a0 = 4.0496 a2 = a0/2.0 c1 = (0, a2, a2) c2 = (a2, 0, a2) c3 = (a2, a2, 0) from ase import Atoms pcell = [c1, c2, c3] box1 = Atoms(cell = pcell, pbc = True) from ase import Atom atom1 = Atom('Al', (0.0, 0.0, 0.0)) box1.append(atom1)
のように定義される。
電子配置
アルミニウムの原子番号は13であるから、当然電子の個数は13である。この13個の電子が
$$(1s)^2(2s)^2(2p)^6(3s)^2(3p)^1$$
のような電子配置をとっている。3p状態が中途半端につまっているということは、主量子数が3の状態すなわち3sと3pに入っている3個の電子が価電子、主量子数が3未満すなわち1sと2sと2pに入っている10個の電子が内殻電子ということになる。より原子番号の大きな原子、すなわちd状態やf状態が関係してくる場合にはこのように単純には言えないが、Alの場合は単純にこの3個の価電子に対する電子状態だけを計算しておけばよい。スピンの重複度を考えると一つの状態に二つの電子が入れるので、価電子数3の半分を切り上げた2個の状態を最低限計算する必要がある。ところで、結晶の価電子の状態は当然原子の価電子の状態である3sと三つの3p状態、合わせて4個の原子状態が混成した状態であろうとも考えられる。どのような混成が起こっているかわからない以上、一応4個の電子状態を計算しておくのがよいと思われる。
そこで、
from ase.calculators.jacapo import Jacapo solver1 = Jacapo(nbands = 4)
のように定義する。
後はbox1とsolver1を結びつけて、全エネルギーを計算する。
box1.set_calculator(solver1) solver1.calculate() print box1.get_total_energy()
実習2
- エネルギーカットオフの値と全エネルギーの関係をグラフにせよ。
エネルギーカットオフ
箱(単位格子)を周期的に並べる事により電荷密度をフーリエ展開し、同時に波動関数もフーリエ展開してハミルトニアンの行列要素を計算するが、フーリエ展開は無限級数であるので計算機で取り扱うためにはこれをどこかで打ち切らなければならない。打ち切る波数をエネルギーに換算したものをカットオフエネルギーと呼び、次のようにJacapoのコンストラクタに電荷密度についてカットオフエネルギーはdwと波動関数についてカットオフエネルギーはpwというキーワードで設定する。
solver1 = Jacapo(nbands = 4, pw = 150, dw = 250) # plane wave cutoff: 150 eV, density cutoff: 250 eV
数字の単位はeVである。
実習3
- BZKPointsを(1,1,1), (2,2,2), (3,3,3)…と変えながら全エネルギーと状態密度の変化を調べよ。
- 正常終了したプログラムの出力結果のncファイルが存在するディレクトリで次のコマンドを実行する。
$ getdos input_nc_file.nc output_text_file.text
- CyberDuck等でoutput_text_file.textをMac側に転送する。
- Abscissa等でoutput_text_file.textのグラフをつくる。
K点サンプリング
一酸化炭素のような分子の計算の場合、周期的に並べられた箱(Atoms)と箱の間には電子の行き来は無いと考えられるし、また行き来は無いと考えられる程度に箱を大きくしなければならないが、結晶の場合はそもそも箱は結晶の単位格子でしかないから、電子は隣り合う箱の間を行き来する。すなわち「運動量」を持っており、いろいろな運動量についてエネルギーを計算する必要がある。量子力学では運動量は波数kで表されるのでK-Pointなどとも呼ばれる。正確にはブリリュアンゾーン(BZ)の範囲内の連続的な波数について計算する必要があるが、これを有限個のK点で近似する。K点の個数は
solver1 = Jacapo(nbands = 4, kpts = (2, 2, 2), pw = 150, dw = 250) # set the k-points Monkhorst-Pack
のようにJacapoのコンストラクタにkptsキーワードで指定する。
この例ではBZ内に$2\times 2\times 2=8$個のK点をとってその運動量を持った電子のエネルギーを計算する。実際にどのようなK点について計算しているかについては実行結果のファイルの内容を確かめよ。
分子の計算のときは
solver1 = Jacapo(nbands = 4, kpts = (1, 1, 1))
$\vec{p}=\hbar\vec{k}=(0,0,0)$、即ちブリリュアンゾーン内のΓ点についての計算を行う。
状態密度
- 状態密度の定義$$ \rho(\varepsilon)=\displaystyle\sum_{k}\delta(\varepsilon - \varepsilon_{k})$$
- 状態密度データファイルの作成
正常終了したプログラムの出力結果のncファイルが存在するディレクトリで次のコマンドを実行する。$ getdos input_nc_file.nc output_text_file.text
output_text_file.textの中にはエネルギーと状態密度がx-yグラフを描く形式で収められている。これは単なるテキストデータなので適当に加工することも可能。
詳細は別項を参照。
実習4
- ユニットセル(単位格子)の大きさを±10%の範囲で変化させ、単位格子の体積(横軸) vs 全エネルギーの変化(縦軸)のグラフを作成せよ。
ユニットセルの体積
$$ \begin{array}{l} \vec{a}_1=(0,\,\displaystyle\frac{a_0}{2},\,\frac{a_0}{2})\\ \vec{a}_2=(\displaystyle\frac{a_0}{2},\,0,\,\frac{a_0}{2})\\ \vec{a}_3=(\displaystyle\frac{a_0}{2},\,\frac{a_0}{2},\,0)) \end{array} $$
この三つのベクトルがつくる平行六面体に原子が1つ含まれ、1辺が$a_0$の立方体に原子が$N$個含まれるので、ユニットセルの体積は$\displaystyle\frac{a_0^3}{N}$で与えられる。