lectures:numeric15
モンテカルロ法と乱数
モンテカルロ法
- 乱数を用いた計算法の総称
- 数値積分
- 物理現象のシミュレーション
- 在庫管理、交通量、待ち行列などのシミュレーション
- 問題が正攻法で解けないときの最後の手段
例)多重積分
$$ \begin{align} \int_0^1\int_0^1\cdots\int_0^1f(x_1,x_2,\cdots,x_L)dx_1dx_2\cdots dx_L\\ \sim\frac{1}{N^L}\sum_{n_1=0}^{N-1}\sum_{n_2=0}^{N-1}\cdots\sum_{n_L=0}^{N-1}f(\textstyle\frac{n_1}{N},\frac{n_2}{N},\cdots,\frac{n_L}{N}) \end{align} $$ * $N$分割して$L$重積分を行うためには$N^L$回の和の計算が必要
- $L=100$ならば$N=2$でも $2^{100}\simeq 10^{30}$回の和が必要
- 1PFLOPSの計算機=毎秒$10^{15}$回の実数計算が可能
- 1年が$3\times 10^{7}$秒なので$10^{30}\div 10^{15}\div (3\times 10^{7}) = 0.3\times 10^{8}$年
- 1PFLOPSの計算機でも3000万年かかる → モンテカルロ法
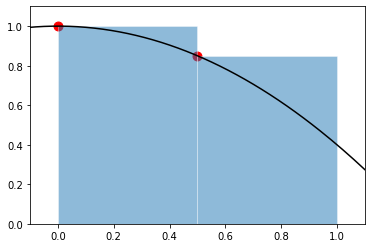
数値積分
$$ \int_a^bf(x)dx\simeq\sum_{k=0}^{N-1}w_kf(x_k) $$
#@title Left Riemann sum import matplotlib.pyplot as plt import numpy as np def f(x): return 1 - 3*x**2/5 xlist = np.arange(-0.2, 1.2, 0.01) ylist = [f(x) for x in xlist] xsample = [0.0, 0.5] ysample = [f(x) for x in xsample] xbar = [0.25, 0.75] # plot fig, ax = plt.subplots() ax.plot(xlist, ylist, color="black") ax.bar(xbar, ysample, width=0.5, edgecolor="white", alpha=.5, linewidth=0.7) ax.scatter(xsample, ysample, s = 80, c = "red") ax.set(xlim=(-0.1, 1.1), ylim=(0, 1.1)) plt.show()
lectures/numeric15.txt · 最終更新: by kimi