lectures:連立一次方程式
文書の過去の版を表示しています。
連立一次方程式
係数行列(拡大係数行列)
$$ \begin{cases} a_{11}x_{1}+a_{12}x_{2}+\cdots+a_{1n}x_{n}=b_{1}\\ a_{21}x_{1}+a_{22}x_{2}+\cdots+a_{2n}x_{n}=b_{2}\\ \vdots\\ a_{n1}x_{1}+a_{n2}x_{2}+\cdots+a_{nn}x_{n}=b_{n} \end{cases} $$
ただ一組の解が存在する場合
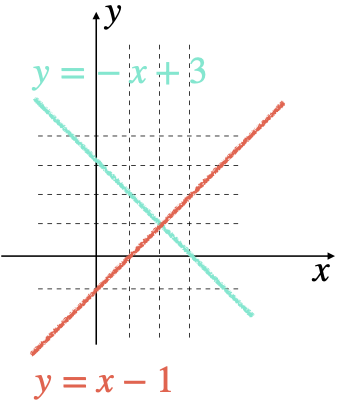 $$
\begin{array}{ll}
&\begin{cases}
x+y=3&\cdots(1)\\
x-y=1&\cdots(2)\\
\end{cases}\\
&\begin{cases}
1x+1y=3&\cdots(1)\\
1x+(-1)y=1&\cdots(2)\\
\end{cases}\\
(2)+(-1)\times(1)\to(2)'&\\
&\begin{cases}
1x+1y=3&\cdots(1)\\
0x+(-2)y=-2&\cdots(2)'\\
\end{cases}\\
(2)'\div(-2)\to(2)''&\\
&\begin{cases}
1x+1y=3&\cdots(1)\\
0x+1y=1&\cdots(2)''\\
\end{cases}\\
(1)+(-1)\times(2)''\to(1)'&\\
\end{array}
$$
$$
\begin{array}{ll}
&\begin{cases}
x+y=3&\cdots(1)\\
x-y=1&\cdots(2)\\
\end{cases}\\
&\begin{cases}
1x+1y=3&\cdots(1)\\
1x+(-1)y=1&\cdots(2)\\
\end{cases}\\
(2)+(-1)\times(1)\to(2)'&\\
&\begin{cases}
1x+1y=3&\cdots(1)\\
0x+(-2)y=-2&\cdots(2)'\\
\end{cases}\\
(2)'\div(-2)\to(2)''&\\
&\begin{cases}
1x+1y=3&\cdots(1)\\
0x+1y=1&\cdots(2)''\\
\end{cases}\\
(1)+(-1)\times(2)''\to(1)'&\\
\end{array}
$$
lectures/連立一次方程式.1683772800.txt.gz · 最終更新: by kimi
