ダイアモンド構造
硅素(シリコン; Si)とゲルマニウム(Ge)の結晶はダイアモンド構造をとる。
炭素(C)がこの構造のように配列したものが、ダイヤモンドである。
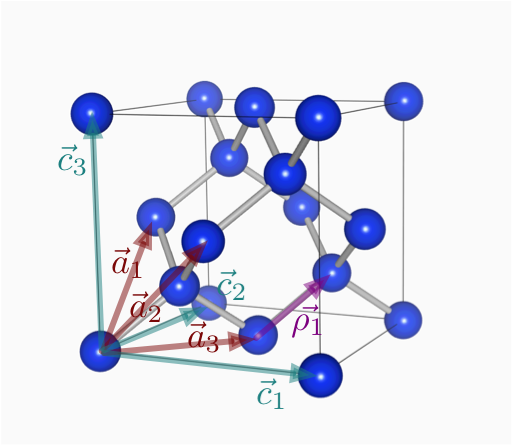
| 原子間距離${b}$ | |
| Si-Si | 2.35Å. |
|---|---|
| Ge-Ge | 2.44Å |
$$ \vec{a}_1=(\frac{c}{2}, \frac{c}{2}, 0) $$ $$ \vec{a}_2=(\frac{c}{2}, 0, \frac{c}{2}) $$ $$ \vec{a}_3=(0, \frac{c}{2}, \frac{c}{2}) $$
基本格子ベクトルと単純基本格子ベクトル
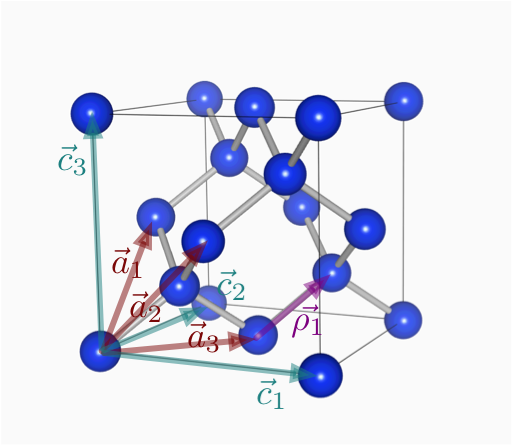 $$
\begin{array}{l}
|\vec{c}_1|=|\vec{c}_2|=|\vec{c}_3|=c\\
\vec{c}_1=(c,\,0,\,0)\\
\vec{c}_2=(0,\,c,\,0)\\
\vec{c}_3=(0,\,0,\,c)\\
|\vec{a}_1|=|\vec{a}_2|=|\vec{a}_3|=a\\
\vec{a}_1=(0,\,\frac{c}{2},\,\frac{c}{2})\\
\vec{a}_2=(\frac{c}{2},\,0,\,\frac{c}{2})\\
\vec{a}_3=(\frac{c}{2},\,\frac{c}{2},\,0)\\
a=\sqrt{\left(\frac{c}{2}\right)^2+\left(\frac{c}{2}\right)^2}=\frac{1}{\sqrt{2}}c\\
\end{array}
$$
$$
\begin{array}{l}
|\vec{c}_1|=|\vec{c}_2|=|\vec{c}_3|=c\\
\vec{c}_1=(c,\,0,\,0)\\
\vec{c}_2=(0,\,c,\,0)\\
\vec{c}_3=(0,\,0,\,c)\\
|\vec{a}_1|=|\vec{a}_2|=|\vec{a}_3|=a\\
\vec{a}_1=(0,\,\frac{c}{2},\,\frac{c}{2})\\
\vec{a}_2=(\frac{c}{2},\,0,\,\frac{c}{2})\\
\vec{a}_3=(\frac{c}{2},\,\frac{c}{2},\,0)\\
a=\sqrt{\left(\frac{c}{2}\right)^2+\left(\frac{c}{2}\right)^2}=\frac{1}{\sqrt{2}}c\\
\end{array}
$$
$$ \begin{array}{l} \vec{\rho}_0=(0,\,0,\,0)\\ \vec{\rho}_1=(\frac{c}{4},\,\frac{c}{4},\,\frac{c}{4})\\ b=\sqrt{\left(\frac{c}{4}\right)^2+\left(\frac{c}{4}\right)^2+\left(\frac{c}{4}\right)^2}=\frac{\sqrt{3}}{4}c\\ \end{array} $$
| a | b | c | |
| Si-Si | 3.84Å | 2.35Å | 5.43Å |
|---|---|---|---|
| Ge-Ge | 3.98Å | 2.44Å | 5.63Å |
有用な関係式
$$ \begin{array}{l} \vec{a}_1=\frac{1}{2}\vec{c}_2+\frac{1}{2}\vec{c}_3\\ \vec{a}_2=\frac{1}{2}\vec{c}_1+\frac{1}{2}\vec{c}_3\\ \vec{a}_3=\frac{1}{2}\vec{c}_1+\frac{1}{2}\vec{c}_2\\ \end{array} $$
$$ \begin{array}{l} \vec{c}_1=-\vec{a}_1+\vec{a}_2+\vec{a}_3\\ \vec{c}_2= \vec{a}_1-\vec{a}_2+\vec{a}_3\\ \vec{c}_3= \vec{a}_1+\vec{a}_2-\vec{a}_3\\ \end{array} $$
$$ \begin{array}{l} \vec{c}_1+\vec{c}_2+\vec{c}_3= \vec{a}_1+\vec{a}_2+\vec{a}_3\\ \vec{\rho_1}=\frac{1}{4}(\vec{c}_1+\vec{c}_2+\vec{c}_3)= \frac{1}{4}(\vec{a}_1+\vec{a}_2+\vec{a}_3)\\ \end{array} $$
