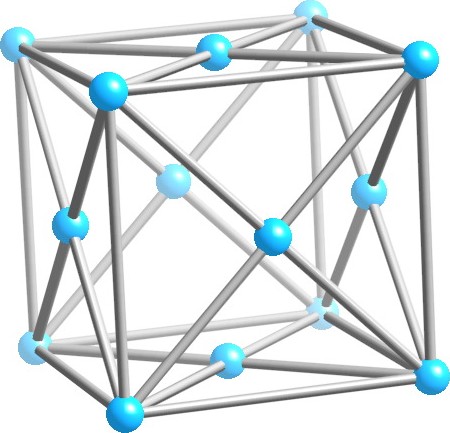
アルミニウム結晶
原子間距離と面間距離
アルミニウム結晶は面心立方格子でありその格子常数(立方体の単位格子をとったときの一辺)は0.40496nm(4.0496Å)である。これを$a_0(=4.0496Å)$とおく
| 格子常数 | $a_0$ | 4.0496Å |
|---|---|---|
| 立方体の一辺 | $a_0$ | 4.0496Å |
| 正方形の対角線 | $b_0=\sqrt{a_0^2+a_0^2}=\sqrt{2}a_0$ | 5.7270Å |
| 立方体の対角線 | $c_0=\sqrt{a_0^2+a_0^2+a_0^2}=\sqrt{3}a_0$ | 7.0141Å |
| 最隣接原子間距離 | $b_0/2$ | 2.8635Å |
| 111格子面間隔 | $c_0/3$ | 2.3380Å |
単純単位格子
単位格子を立方体の形にとると、1の単位格子に4つの原子が含まれている。1の単位格子に1つの原子が含まれるように単位格子をとるには、
$$ \begin{array}{l} \vec{a}_1=(0,\,\frac{a_0}{2},\,\frac{a_0}{2})\\ \vec{a}_2=(\frac{a_0}{2},\,0,\,\frac{a_0}{2})\\ \vec{a}_3=(\frac{a_0}{2},\,\frac{a_0}{2},\,0)) \end{array} $$
のように単位格子ベクトルをとればよい。したがって、計算で用いるListOfAtomsオブジェクトは
a0 = 4.05 from math import sqrt a2 = a0/2. c1 = (0, a2, a2) c2 = (a2, 0, a2) c3 = (a2, a2, 0) pcell = [c1, c2, c3] from ASE import Atom, ListOfAtoms bulk = ListOfAtoms([Atom('Al',(0, 0, 0))]) bulk.SetUnitCell(pcell)
のように定義される。
電子配置
アルミニウムの原子番号は13であるから、当然電子の個数は13である。この13個の電子が
$$(1s)^2(2s)^2(2p)^6(3s)^2(3p)^1$$
のような電子配置をとっている。3p状態が中途半端につまっているということは、主量子数が3の状態すなわち3sと3pに入っている3個の電子が価電子、主量子数が3未満すなわち1sと2sと2pに入っている10個の電子が内殻電子ということになる。より原子番号の大きな原子、すなわちd状態やf状態が関係してくる場合にはこのように単純には言えないが、Alの場合は単純にこの3個の価電子に対する電子状態だけを計算しておけばよい。スピンの重複度を考えると一つの状態に二つの電子が入れるので、価電子数3の半分を切り上げた2個の状態を最低限計算する必要がある。ところで、結晶の価電子の状態は当然原子の価電子の状態である3sと三つの3p状態、合わせて4個の原子状態が混成した状態であろうとも考えられる。どのような混成が起こっているかわからない以上、一応4個の電子状態を計算しておくのがよいと思われる。
そこで、
from Dacapo import Dacapo calc = Dacapo(nbands = 4)
のように定義する。
calc.SetBZKPoints((2,2,2)) # set the k-points Monkhorst-Pack calc.SetPlaneWaveCutoff(150) # planewavecutoff in eV