コバルト(0001)表面の水素原子吸着
from math import sqrt a = 2.5 c = 1.622*a a1 = (2*a, 0, 0 ) a2 = (a, a*sqrt(3), 0 ) a3 = (0, 0, 3*c) from ase import Atom, Atoms from ase.calculators.jacapo import Jacapo from ase.dft.kpoints import cc18_1x1 slab = Atoms(pbc = True) slab.append(Atom('Co', (0, 0, 0), magmom=1.6)) slab.append(Atom('Co', (1/2., 0, 0), magmom=1.6)) slab.append(Atom('Co', (0, 1/2., 0), magmom=1.6)) slab.append(Atom('Co', (1/2., 1/2., 0), magmom=1.6)) slab.append(Atom('Co', (1/6., 1/6., -1/6.), magmom=1.6)) slab.append(Atom('Co', (2/3., 1/6., -1/6.), magmom=1.6)) slab.append(Atom('Co', (1/6., 2/3., -1/6.), magmom=1.6)) slab.append(Atom('Co', (2/3., 2/3., -1/6.), magmom=1.6)) slab.set_cell([a1, a2, a3], scale_atoms = True) slab.append(Atom('H', (0, 0, 1.4598))) para = {} para.update(kpts = cc18_1x1) # set the k-points (Chadi-Cohen) para.update(pw = 340) # planewavecutoff in eV para.update(dw = 340) para.update(nbands = 10 + 8*6 + 1*1) # set the number of electronic bands para.update(spinpol = True) # this calculation should be spinpolarized para.update(symmetry = True) # use symmetry to reduce the k-point set para.update(atoms = slab) calc = Jacapo('H_Co_ontop.nc', **para) energy = calc.get_potential_energy() print 'energy = ', energy
energy = -8741.97691323
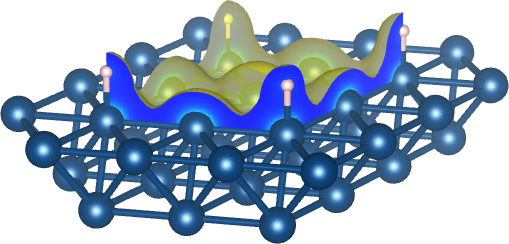
$ nc2cube H_Co_ontop.nc H_Co_ontop.cube
