第一原理計算実習

未整理計算結果

第一原理計算は強力な¹⁾道具ではあるが、決して万能ではない。常に、次のようなことに留意せよ。

第一原理計算の注意点

• エネルギーの絶対値は信用できない。異なる原子配置間のエネルギー差は結構信用できる。²⁾
• エネルギー差を問題にするときは原子数・電子数・計算条件をそろえること。
• 個々の固有値の絶対値やその差は全く当てにならない。したがってエネルギーギャップなどは求まらない。
• 原子配置の変化に対する、特定の固有値の変化は結構意味がある。³⁾
• 波数の変化に対する、特定の固有値の変化は結構意味がある。⁴⁾

最も簡単な計算の例として、一酸化炭素(CO)の一点計算を行う→実習

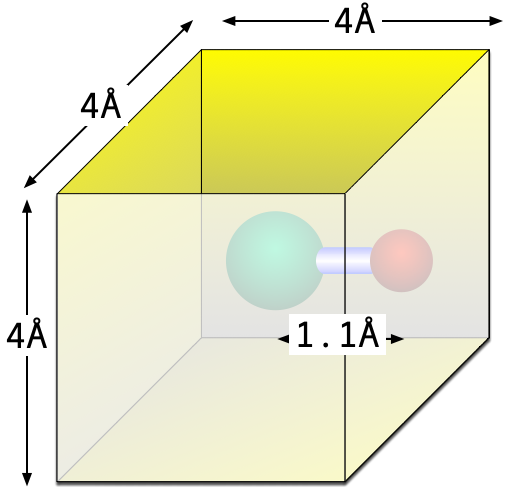
- 一酸化炭素(CO)の断熱ポテンシャル 時刻<latex>{t}</latex>における炭素の位置を${x(t)}$、酸素の位置を${y(t)}$、酸素と炭素がバネでつながっていると考えてそのバネ定数を${K}$とする。ただし、酸素と炭素の位置はバネが伸びも縮みもしていない状態すなわち力が働いていない状態からのずれで表わすことにする。このとき、全エネルギーは $$ E = \frac{1}{2}M\left( {\frac{{{\rm{d}}x}}{{{\rm{d}}t}}} \right)^2 + \frac{1}{2}m\left( {\frac{{{\rm{d}}y}}{{{\rm{d}}t}}} \right)^2 + \frac{1}{2}K\left( {x\left( t \right) - y\left( t \right)} \right)^2 $$ で与えられる。 $$ M\displaystyle\frac{{{\rm{d}}^2 }}{{{\rm{d}}t^2 }}x\left( t \right) = - K\left( {x\left( t \right) - y\left( t \right)} \right) \\ $$

$$ m\displaystyle\frac{{{\rm{d}}^2 }}{{{\rm{d}}t^2 }}y\left( t \right) = - K\left( {y\left( t \right) - x\left( t \right)} \right) \\ $$

$$ x\left( t \right) = x_0 {\rm{e}}^{ - i\omega t} $$

$$ y\left( t \right) = y_0 {\rm{e}}^{ - i\omega t} $$

$$ - M\omega ^2 x_0 {\rm{e}}^{ - i\omega t} = - K\left( {x_0 {\rm{e}}^{ - i\omega t} - y_0 {\rm{e}}^{ - i\omega t} } \right) $$

$$ - m\omega ^2 y_0 {\rm{e}}^{ - i\omega t} = - K\left( {y_0 {\rm{e}}^{ - i\omega t} - x_0 {\rm{e}}^{ - i\omega t} } \right) $$

1. CO₂の伸縮振動の振動数を求めよ。→演習
2. COとCO₂でバネ定数に相当するものを比較せよ。→演習

　- 一酸化炭素(CO)の構造最適化

1. H₂OのO-H間距離とH-O-Hの角度を求めよ。→演習
2. SiH₄のSi-H間距離を求めよ。→演習

1. アルミニウム結晶
2. bcc鉄の磁気的性質

1. シリコン結晶の安定な格子常数を求めよ。→演習
2. 面心立方構造の鉄結晶について磁気的性質を調べよ。→演習

1. Al(001)面
2. Al(111)面
3. Al(110)面

• コバルト(111)表面の水素吸着
• Si(111)表面

• 銅結晶