Chips & Tips

チップじゃないんだ，ティップなんだよ！

a small piece or part serving as an end, cap, or point
an item of expert or authoritative information
a gift or money tendered for a service performed or anticipated

a small thin and flat piece
something small, worthless, or trivial
one of the counters used as a token for money in poker and other games

でどっちなの？

「支払方法なし」でapple idを登録する

AppStoreを立ち上げる
サインオフする（サインインしていないことを確かめる）
無料アプリをひとつインストールしようとする（Evernote辺がお勧め）
サインインを求められるのでこのダイアログの中の「Apple IDを登録」ボタンを押す
支払方法には「なし」を選択してApple IDを作成する
メールを受け取りApple IDをアクティベートする

App Store以外からダウンロードしてきたアプリケーションを起動する

App Store以外のサイトからダウンロードしてきたアプリケーションを起動しようとすると、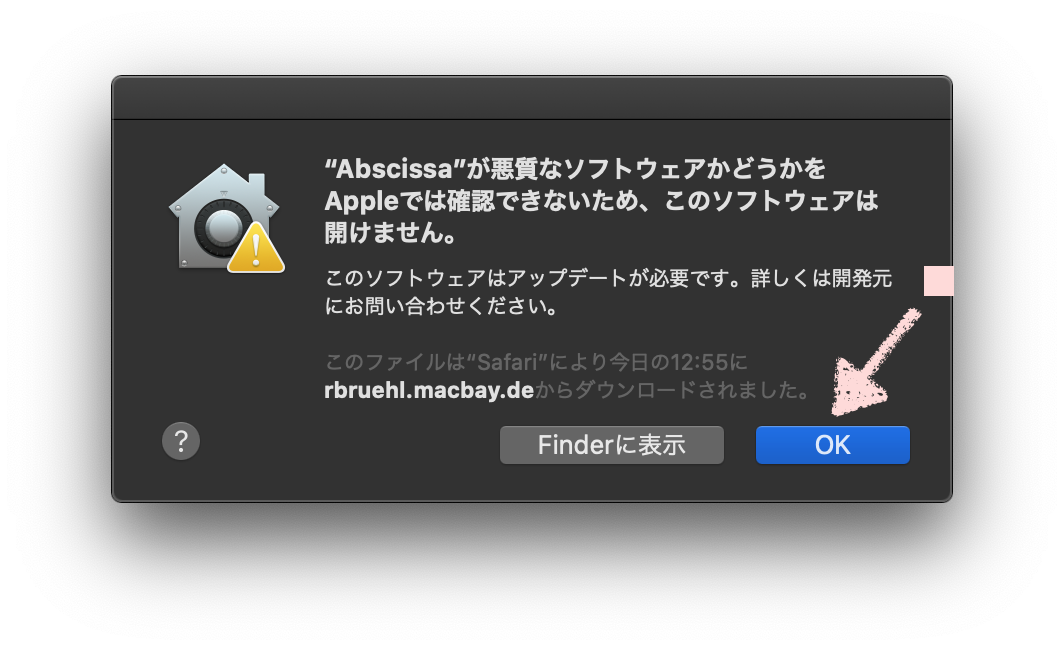上図のようなダイアログが起動しアプリケーションが起動できないことがあります。

このような場合は「OK」ボタンをクリックした後すぐに「システム環境設定」を起動し、「セキュリティとプライバシー」タグを開きます。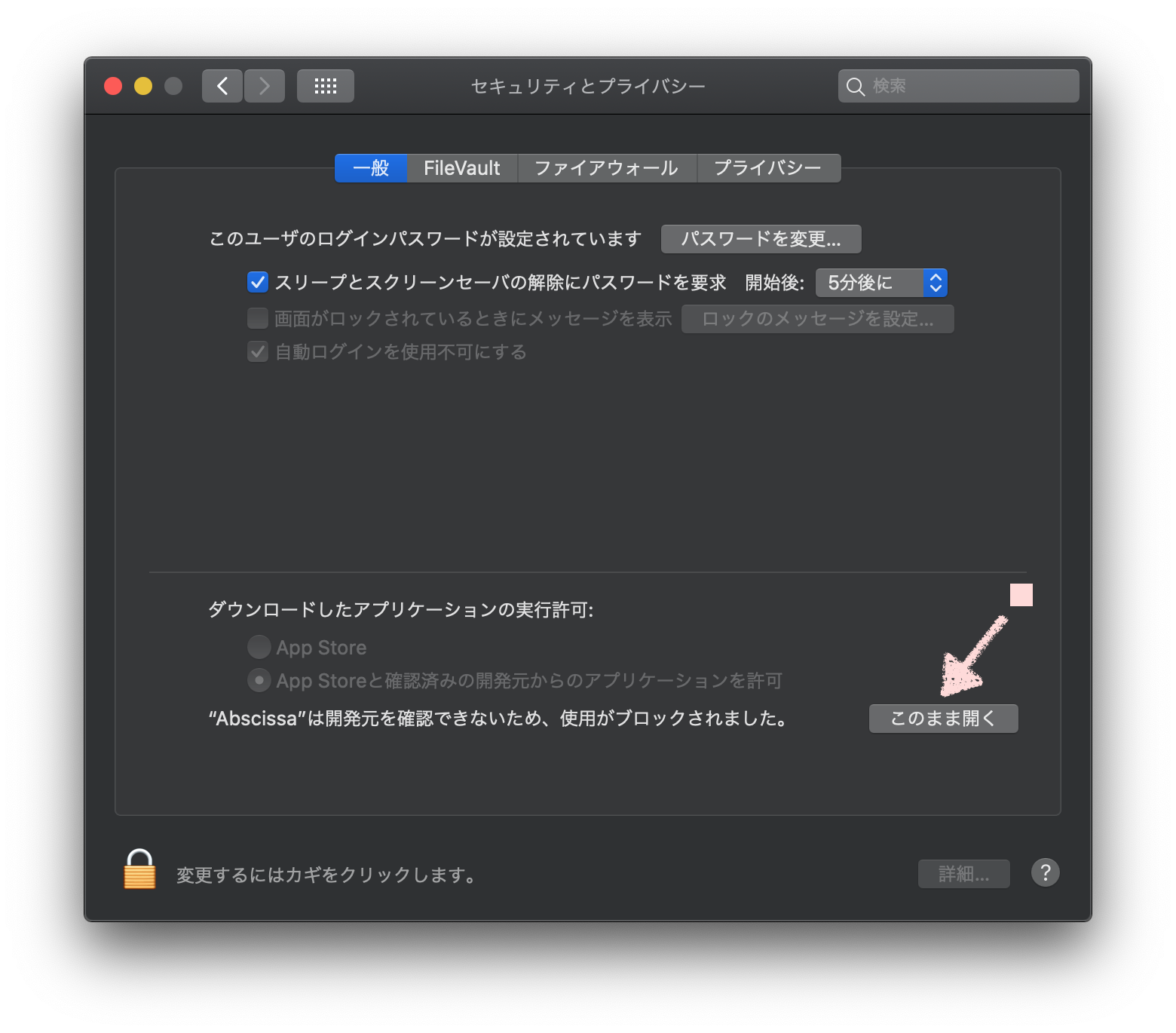右下のあたりに「このまま開く」ボタンがありますから、これをクリックします。そうすると再度アプリケーションが起動され、今度は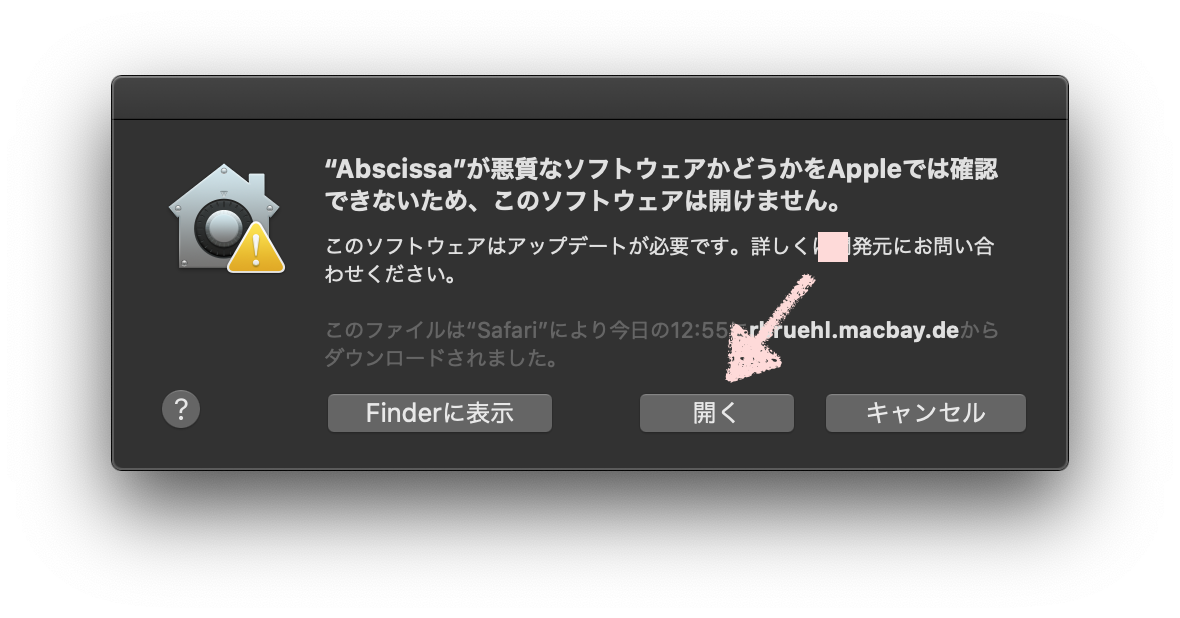上図のように「開く」ボタンが選択可能になっていますから、これをクリックします。

この作業は一回行っておくと次回からは即座に起動できるようになります。

大文字小文字変換

$ tr [A-Z] [a-z] < 混在ファイル名 > 小文字のみファイル名

旧月名

睦月／如月／弥生／卯月／皐月／水無月／文月／葉月／長月／神無月／霜月／師走

nslookupでMX引き

imia:~ t05e068$ man nslookup
imia:~ t05e068$ nslookup - 150.55.31.253
> set querytype=MX   
> sst.ee.ous.ac.jp
Server:		150.55.31.253
Address:	150.55.31.253#53
 
sst.ee.ous.ac.jp	canonical name = sstmail.ee.ous.ac.jp.
sstmail.ee.ous.ac.jp	mail exchanger = 100 ns28a.ee.ous.ac.jp.
sstmail.ee.ous.ac.jp	mail exchanger = 10 sstmail.ee.ous.ac.jp.
> std.ous.ac.jp
Server:		150.55.31.253
Address:	150.55.31.253#53
 
Non-authoritative answer:
std.ous.ac.jp	mail exchanger = 10 doctor.ous.ac.jp.
 
Authoritative answers can be found from:
std.ous.ac.jp	nameserver = ipc10ssv4.std.ous.ac.jp.
std.ous.ac.jp	nameserver = ipcallsv.std.ous.ac.jp.
doctor.ous.ac.jp	internet address = 150.55.4.244

note plug-in

note: noteを挿入する

default:

<jmol si.pdb.gz></jmol>

と記述することでjmolプラグインを使用できる

important: pdbファイルはアップロードする際に必ずgzipで圧縮しておかなければならない

tip: jmolの枠の中で右クリックすると各種設定ができる

warning: 一つのページに複数のjmolプラグインを記述すると結構重くなる。重さを確認せずに、いきなり3つ以上のjmolプラグインを記述することを禁止する

MathJax plugin

latex: tex形式で数式をかく

$$ \frac{3}{4 \pi} \sqrt{4 \cdot x^2 12} $$

$$ \lim_{n \to \infty} \displaystyle\sum_{k=1}^n \frac{1}{k^2} = \frac{\pi^2}{6} $$

$$ \it{f}(x) = \frac{1}{\sqrt{x} x^2} $$

$$ e^{i \pi} + 1 = 0\; $$

DokuWiki標準 code

code: ソースコードを書く

c

#include <stdio.h>
int main(void) {
  printf("Hello, world\n");
  return 0;
}

fortran

program hello
  write (*, *) "Hello, world"
  stop
end program

python

  from ASE import Atom
  a = Atom('H', (0, 0 0), tag = 1)

目次