連立一次方程式

$$ \begin{cases} a_{11}x_{1}+a_{12}x_{2}+\cdots+a_{1n}x_{n}=b_{1}\\ a_{21}x_{1}+a_{22}x_{2}+\cdots+a_{2n}x_{n}=b_{2}\\ \vdots\\ a_{n1}x_{1}+a_{n2}x_{2}+\cdots+a_{nn}x_{n}=b_{n} \end{cases} \Rightarrow \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}&\,&b_{1}\\ a_{21}&a_{22}&\cdots&a_{2n}&\,&b_{2}\\ \vdots&\vdots&\ddots&\vdots&&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}&\,&b_{n} \end{bmatrix} $$

• ある行を何倍かする（0倍以外）
• ある行の何倍かを他の行に加える
• ある行と別の行を交換する

$$ \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}&\,&b_{1}\\ a_{21}&a_{22}&\cdots&a_{2n}&\,&b_{2}\\ \vdots&\vdots&\ddots&\vdots&&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}&\,&b_{n} \end{bmatrix} \Rightarrow \begin{bmatrix} 1&\ast&\cdots&\ast&\,&\ast\\ 0&1&\cdots&\ast&\,&\ast\\ \vdots&\vdots&\ddots&\vdots&&\vdots\\ 0&0&\cdots&1&\,&\ast \end{bmatrix} $$

• ただ1組の解をもつ

$$ \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}&\,&b_{1}\\ a_{21}&a_{22}&\cdots&a_{2n}&\,&b_{2}\\ \vdots&\vdots&\ddots&\vdots&&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}&\,&b_{n} \end{bmatrix} \Rightarrow \begin{bmatrix} 1&\ast&\cdots&\ast&\,&\ast\\ 0&1&\cdots&\ast&\,&\ast\\ \vdots&\vdots&\ddots&\vdots&&\vdots\\ 0&0&\cdots&0&\,&0 \end{bmatrix} $$

• 解は無数に存在する（解にはパラメータが含まれる）

$$ \begin{bmatrix} a_{11}&a_{12}&\cdots&a_{1n}&\,&b_{1}\\ a_{21}&a_{22}&\cdots&a_{2n}&\,&b_{2}\\ \vdots&\vdots&\ddots&\vdots&&\vdots\\ a_{n1}&a_{n2}&\cdots&a_{nn}&\,&b_{n} \end{bmatrix} \Rightarrow \begin{bmatrix} 1&\ast&\cdots&\ast&\,&\ast\\ 0&1&\cdots&\ast&\,&\ast\\ \vdots&\vdots&\ddots&\vdots&&\vdots\\ 0&0&\cdots&0&\,&\ast \end{bmatrix} $$

• 解は存在しない

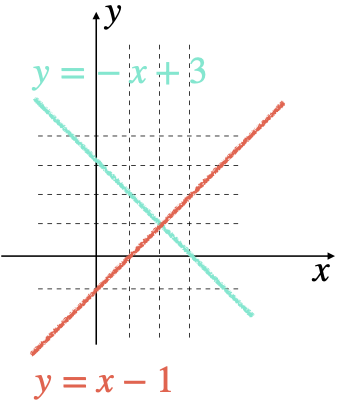$$ \begin{array}{ll} &\begin{cases} x+y=3&\cdots(1)\\ x-y=1&\cdots(2)\\ \end{cases}\\ &\begin{cases} 1x+1y=3&\cdots(1)\\ 1x+(-1)y=1&\cdots(2)\\ \end{cases}\\ (2)+(-1)\times(1)\to(2)'&\\ &\begin{cases} 1x+1y=3&\cdots(1)\\ 0x+(-2)y=-2&\cdots(2)'\\ \end{cases}\\ (2)'\div(-2)\to(2)''&\\ &\begin{cases} 1x+1y=3&\cdots(1)\\ 0x+1y=1&\cdots(2)''\\ \end{cases}\\ (1)+(-1)\times(2)''\to(1)'&\\ \end{array} $$