目次
疑似乱数
- 乱数
- でたらめに並んだ数字の列
- サイコロを振る
- 正20面体サイコロ
- 物理現象を利用する
- 放射線、電流のノイズ
- 国勢調査などの中から数字を抜き出す
- 疑似乱数
- ある規則に従って「乱数のようなもの」を作る
- 計算機などを用いて生成した
でたらめに近い数字の列
- 再現性
- 周期性
(一様)疑似乱数
- 乱数の性質のうちいくつかを再現する数列
- それぞれの数が出現する頻度が一様
- (一桁の整数の乱数) 5の次に6が来る頻度は1/10
- (0と1の乱数) 長さn+1の連の個数と長さnの連の個数の比は1/2
- 一部を取り出しても偏りがない。 ⇒ 局所ランダム性
- 一様乱数の発生法
- 線形合同法
- Lagged Fibonacci法
- M系列法
- Mersenne Twister法
線形合同法
線形合同法
- Lehmer, 1948)
$$X_n= (aX_{n-1}+c) \pmod M$$
乗算合同法
$$X_n= (aX_{n-1}) \pmod M$$
| $M$ | 法 | $0<M$ |
| $a$ | 乗数 | $0<a<M$ |
| $c$ | 増分 | $0<c<M$ |
| $X_0$ | 初期値 | $M0<X_0<M$ |
線形合同法の例
- $c = 0$, $a = 11$, $M = 2^5 = 32$, $X_0 = 1$
$$ \begin{matrix} & & 1\\ 1*11 \pmod {32} & &= 11\\ 11*11 \pmod {32} &= 121 \pmod {32} &= 25\\ 25*11 \pmod {32} &= 275 \pmod {32} &= 19\\ 19*11 \pmod {32} &= 209 \pmod {32} &= 17\\ 17*11 \pmod {32} &= 187 \pmod {32} &= 27\\ 27*11 \pmod {32} &= 297 \pmod {32} &= 9\\ 9*11 \pmod {32} &= 99 \pmod {32} &= 3\\ 3*11 \pmod {32} &= 33 \pmod {32} &= 1 \end{matrix} $$
- 周期:8
線形合同法の特徴
- $0$から$M–1$の間の整数の乱数を生成する
- $n$番目の乱数は$n–1$番目の乱数により決まる
- 最大周期は$M$である
- 1周期の中に同じ数は2度出てこない
- $a$と$M$は互いに素にとらないと充分にデタラメにならない
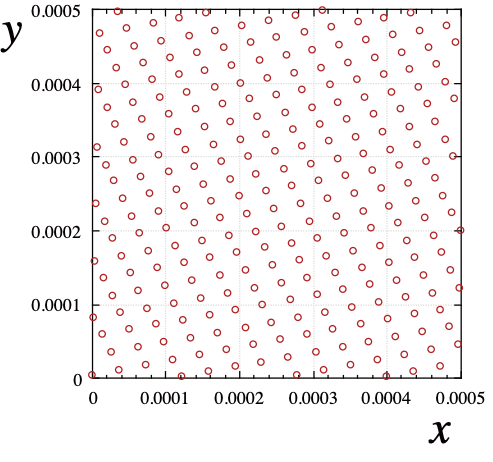
- 結晶構造になる
実数の一様乱数
- $[0, M–1]$の乱数$\{x_i\}$を$[0, 1)$の乱数$\{u_i\}$に変換
- $ u_i = \displaystyle\frac{x_i}{M}$
例)$c = 0$, $a = 177$, $M = 2^15$, $X_0 = 1$
| $n$ | $x_n$ | $u_n$ |
|---|---|---|
| 0 | 1 | 0.00003051758 |
| 1 | 177 | 0.00540161133 |
| 2 | 31329 | 0.95608520508 |
| 3 | 7441 | 0.22708129883 |
| 4 | 6337 | 0.19338989258 |
線形合同法の実装系
- $X_n = (aX_{n–1} + c) \pmod M$
rand(cの元標準乱数)- $a=1103515245$, $c=12345$, $M=2^{31}$ (BSD)
drand48(randの代替標準乱数)- $a=25214903917$, $c=11$, $M=2^{48}$
Lagged Fibonacci法
$$X_n=f(X_{n-r}, X_{n-s}) \pmod M$$
$r$, $s$, $M$: 整数($r>s$)
- 周期は最大$(2^w–1)(2^r–1)$($w$はワード長)
- 連続する乱数の和の分布が正規分布からずれる
Lagged Fibonacci法の実装系
M系列法(線形最大周期列法)
- Maximum length linearly recurring sequence
$$R_n=R_{n-p}\oplus R_{n-q}$$
- 周期は$2^p–1$で比較的長い。
- 演算が単純⇒高速
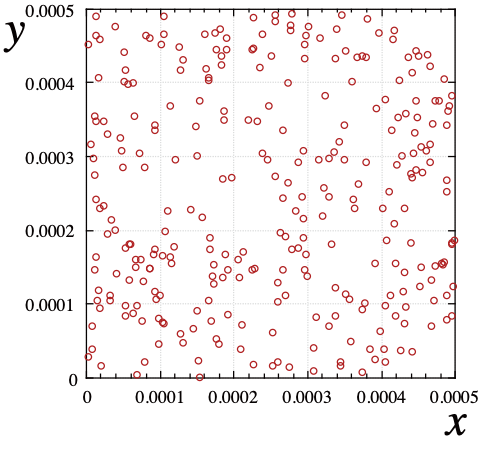
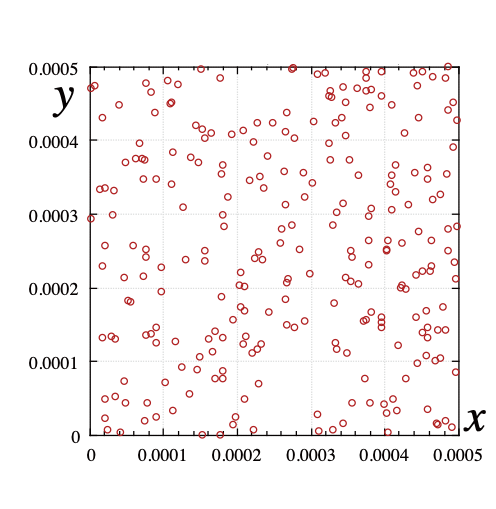
- 結晶構造にならない。
| $p$ | $q$ |
|---|---|
| 89 | 38 |
| 127 | 1, 7, 15, 30, 63 |
| 250 | 103 |
| 521 | 32, 48, 158, 168 |
| 607 | 105, 147, 273 |
Mersenne-Twister法
- 松本-西村 1997
- $x_{n+p} = x_{n+q}\oplus x_{n+1}B\oplus x_n A$
- $A$, $B$ ある特別な$w\times w$行列
- $p$, $q$ はある特別な整数
- 周期は $2^{19937}–1$
- 623次元空間で均等に分布
分布をもった乱数
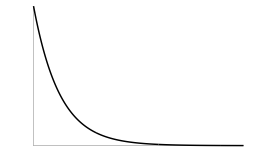
指数分布
逆関数法
- $\{u_i\}$ $(0\le u_i<1)$: 一様乱数
- $x_i=-\displaystyle\frac{1}{\lambda}\ln {u_i}$
- $\{x_i\}$: $f(x)\propto \mathrm{e}^{-\lambda x}$の指数分布に従う乱数
正規分布
極座標法(Box-Muller 法)
- $\{u_i\}$, $\{v_i\}$ $(0\le u_i, v_i<1)$: 一様乱数
- $x_i=\sqrt{-2\ln {u_i}}\cos{(2\pi v_i)}$
- $y_i=\sqrt{-2\ln {u_i}}\sin{(2\pi v_i)}$
- $\{x_i\}$, $\{y_i\}$: 平均0, 標準偏差1の正規分布に従う乱数
中心極限定理
- $\{u_i\}$ $(0\le u_i<1)$: 一様乱数
- $x_k=(u_{12k}+u_{12k+1}+u_{12k+2}+\cdots+u_{12k+10}+u_{12k+11})-6$
- $\{x_i\}$: 平均0, 標準偏差1の正規分布に従う乱数